(UERJ 2014) Considere uma placa retangular ABCD de acrílico, cuja diagonal AC mede 40 cm.
Um estudante, para construir um par de esquadros, fez dois cortes retos nessa placa nas direções AE e AC, de modo que DÂE = 45º e BÂC = 30º, conforme ilustrado a seguir:
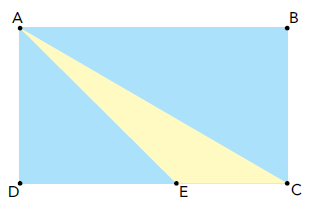
Após isso, o estudante descartou a parte triangular CAE, restando os dois esquadros.
Admitindo que a espessura do acrílico seja desprezível e que \(\sqrt3 = 1,7\), a área, em \(cm^2\), do triângulo CAE equivale a:
(A) 80
(B) 100
(C) 140
(D) 180
Respostas
rafael lopes
há 7 anos
tem que subtrair a área do triangulo ADC do triangulo ADE
AC =40cm
DC=AB=40cm x cos30°=40cm x √3/2=34cm
AD=BC=40cm x sen30°=40cm x 1/2=20,0 cm
como DÂE = 45° então AD=DE=20cm
area do triangulo ADC= (34 X 20)/2=340 cm^2
area do triangulo ADE= (20 X 20)/2=200 cm^2
340-200 = 140 cm^2
Crie sua conta grátis para liberar essa resposta. 🤩
Já tem uma conta?
Ao continuar, você aceita os Termos de Uso e Política de Privacidade
Andre Pucciarelli
há 7 anos
Sabendo que temos um retângulo, AB=CD e AD=BC.
Pela soma dos ângulos dos triângulos, BCA=60º e AED=45º.
O lado AB é dado por:
\(AB=sen(30).40=20\)
O lado AD é:
\(AD=cos(30).40=20 \sqrt 3\)
A área do triângulo retângulo ABC e ADE:
\(A_{abc}={ab.ad \over 2}=200 \sqrt 3\\ A_{ade}={AD.AD \over 2}=200\)
Resposta: Pela diferença de áreas, teremos:
\(400.1,7-(200.1,7)+200=140\)
Alternativa C.
Ainda com dúvidas?
Envie uma pergunta e tenha sua dúvida de estudo respondida!
Mais conteúdos dessa disciplina
Literatura Infantil na Educação- Contação de Histórias na Educação
- Experimentação Agrícola
- Qual dos seguintes aspectos é considerado crítico para a segurança da informação em uma iniciativa de BI? Questão 22Escolha uma opção: a. Frequência d
- 5. Em um contrato de custos reembolsáveis, qual modalidade apresenta o maior risco financeiro para o comprador, pois o lucro do fornecedor aumenta à m
- Considerando os desafios impostos pela pobreza, desigualdade e exclusão no Brasil, qual o significado de ES, conforme o que foi abordado nesse módulo?
- 15.Caio e Matheus, policiais militares, foram orientados, pelo superior hierárquico, para que realizassem patrulhamento de rotina na região Da Praça C
- magine que seja construída uma casinha de bonecas em uma escala 1:12 em relação a uma casa de verdade. Isso significa que cada medida (como altura,...
- A fatoração de números em suas bases primas é uma técnica útil em logaritmos. Se considerarmos 128 e 125, que são 2^7 e 5^3, respectivamente, qual ...
- Os logaritmos têm aplicações práticas em diversas áreas, incluindo a engenharia e a ciência. Se considerarmos a equação t × log(1,28/1,25) = log(5)...
- A manipulação algébrica de logaritmos pode ser desafiadora. Se t = log(5) / (log(128) - log(125)), qual é a forma simplificada de t após aplicar a ...
- A manipulação de logaritmos é uma habilidade essencial em matemática avançada. Se t = log(5) / (log(128) - log(125)), qual é a importância de enten...
- A compreensão das propriedades dos logaritmos é fundamental para resolver problemas matemáticos. Se t = log(5) / (log(128) - log(125)), qual é a in...
- ntre as medidas de dispersão conhecidas, a mais simples de calcular é a amplitude de variação (a), que pode ser definida como a diferença entre os...
- Qua a resposta a essa questão? têm aplicações, por exemplo, na determinação de velocidades de veículos nas ruas e rodovias. Já os sonares são emissor
- Considere as alternativas abaixo e destaque aquela que apresenta uma característica do sistema jurídico que exerceu influência nos diferentes tipos...
- ZJJQZD teste prova ZJJQZD
- ZJMLV1 teste prova ZJMLV1