PRECISO DA RESOLUÇÃO

---

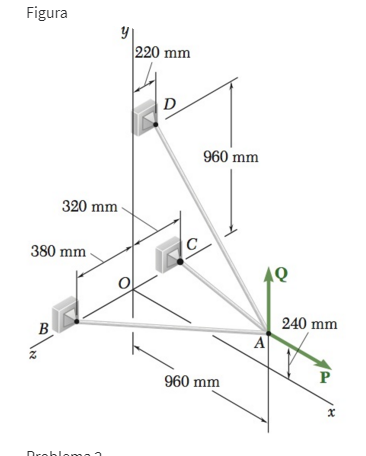
Passo 1. Referencial:

Nesse caso, ele foi dado, e é Oxyz.

---

Passo 2. Tabela de pontos:

A tabela de pontos nada mais é do que os pontos da figura, serem escritos em coordenadas, de acordo com o referencial.

Nesse caso, as distancias estão em milímetros:

PONTO	X	Y	Z
A	960	240	0
B	0	0	380
C	0	0	-320
D	0	960	-220
O	0	0	0

 

 

 

 

 

---

Passo 3. Forças escritas vetorialmente:

      3.1 Força P:

      A força P está paralela ao eixo x, e seu módulo é nossa incógnita, que chamaremos de P

      Se ela está paralela a x, vetorialmente, ela é escrita como 

      3.2 Cabo AB:

      Esse cabo possui uma força de tração que vai do ponto A ao ponto B. Podemos escrever essa tração por meio da fórmula:

\(AB\cdot \frac{B-A}{|B-A|}\)      

\(AB\cdot \frac{(-960,~ -240,~ 380)}{\sqrt{(-960)^2+(-240)^2+380^2}}\)

\(AB\cdot \frac{(-960,~-240,~380)}{1060}\)

\(AB\cdot (-0,905;~-0,226;~0,358)\)

     3.3 Cabo AC:

      Esse cabo possui uma força de tração que vai do ponto A ao ponto C. Podemos escrever essa tração por meio da fórmula:

\(AC\cdot \frac{C-A}{|C-A|}\)

\(AC\cdot \frac{(-960,~ -240,~ -320)}{\sqrt{(-960)^2+(-240)^2+(-320)^2}}\)

\(AC\cdot \frac{(-960,~-240,~-320)}{1040}\)

\(AC\cdot (-0,923;~-0,230;~-0,307)\)

3.2 Cabo AD:

      Esse cabo possui uma força de tração que vai do ponto A ao ponto D. Podemos escrever essa tração por meio da fórmula:

\(AD\cdot \frac{D-A}{|D-A|}\)

Para esse cabo, porém, já sabemos o módulo da tração, que é 305N. Acharemos portanto, seu valor numérico em coordenadas:

\(305\cdot \frac{(-960,~720,~-220)}{\sqrt{(-960)^2+720^2+(-220)^2}}\)

\(305\cdot \frac{(-960,~720,~-220)}{1220}\)

\((-240,180,-55)\)

---

Passo 4: Tabela de forças:

Essa tabela possui as forças que achamos, escritas vetorialmente:

FORÇA	i	j	k
	P	0	0
	-0,905AB	-0,226AB	0,358AB
	-0,923AC	-0,230AC	-0,307AC
	-240	180	-55
	0	0	0

 

 

 

 

 

 

---

Passo 5: Equações e sistema:

Uma vez que o sistema está em equilíbrio, a resultante das forças tem que ser zero.

Para que tudo dê zero, basta somarmos cada coordenada da tabela, e igualarmos a zero. Aaasim:

\(\left\{\begin{matrix} P-0,905AB-A,923AC-240=0(i) \\ -0,226AB-0,230AC+180=0(ii)~~~~~~ \\ 0,359AB-0,307AC-55=0(iii)~~~~~~~~~~ \end{matrix}\right.\)

Agora, isolemos AB da equação (iii):

\(AB=\frac{55+0,307AC}{0,359}\)

Substituindo AB em (ii), temos:

\(-0,226(\frac{55+0,307AC}{0,359})-0,307AC+180=0 \\ -34,623-0,193AC-0,307AC+180=0 \\ 145,377-0,5AC=0 \\ AC=290,754N\)

Portanto:

\(AB=\frac{55+0,307\cdot 290,754}{0,359} \\ AB= 401,842N\)

Então:

\(P=0,905\cdot401,842+0,923\cdot290,754+240 \\ P=872,032N\)

OBS.: TODOS OS CÁLCULOS FORAM TRUNCADOS NA TERCEIRA CASA APÓS A VÍRGULA